Събиране на данни за електрически превозни средства – сензори

Системи за събиране на данни

Системите за събиране на данн – сензорите и управлението на електрическите превозни средства наблягат на сензорите, микропроцесорите и цифровите комуникационни системи, използвани в съвременните превозни средства, за да оптимизират работата на превозното средство. Темите включват преглед на теорията на електричеството и електрониката, транзистори, портали, теория на мрежите на превозното средство, вградени контролери и комуникационни протоколи в превозните средства, сензори, задвижващи механизми, основните системи в превозните средства с вътрешно горене и електрическо задвижване или помощни електрически превозни средства, емисии на превозните средства и системите за контрол на емисиите, както и избрани теми в управлението на мощността. Използвайки инструменти за мрежов анализ, студентът ще придобие широки познания за мрежите и комуникациите, използвани в съвременните автомобилни системи.

 

Работа с булева алгебра и числови системи (1 от 2)

Определете стойността, и резултата от булевите оператори.

Този урок прави преглед на математическите концепции за булева алгебра и системи за номериране, за да ви помогне да разберете ключовите функции на електрическите превозни средства. Първо, ще анализираме прости булеви оператори, за да разберем как се осъществява превключването на базата на транзистор и порта в превозните средства. След това ще разгледаме приликите между включване/изключване на превключвателите и системата за включване/изключване на двоично номериране. И накрая, ще практикуваме работа с двоични и шестнадесетични бройни системи, използвани от електрическата комуникационна система в превозните средства, наречена контролерна зона (CAN).

Уравненията за два основни булеви оператора (И и ИЛИ) могат да се разглеждат като еднополюсни превключватели последователно или паралелно.

Булева алгебра и превключващи електрически вериги

Много електронни системи се превключват не с механични ключове, а с транзистори, подредени последователно или паралелно. Малко напрежение и ток в два от трите проводника контролират голямо напрежение или ток през изходната страна на транзистора.

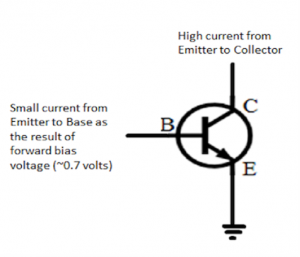
Фигура 1. Схематично представяне на транзистор отрицателно-положително-отрицателен (NPN), използван като ключ.

За NPN транзистора, показан на фигура 1, малкото преднапрежение от около 0,7 волта, с основата (B) при по-високо напрежение от емитера (E), контролира по-голям ток от емитера към колектора (C). Ако връзката емитер-база не е насочена напред, веригата емитер-колектор няма да провежда електричество и е изключена. По този начин транзисторът се използва като електронен ключ или реле, за да се избегне образуването на дъга на постоянен ток в механичен превключвател, доставящ ток от батерията към товара. Такава дъга може да възникне, ако се използва механичен ключ за директно управление на тока във веригата колектор-емитер.

Друго полезно полупроводниково устройство е гейт , в който два изхода се сравняват с помощта на булева алгебра. Както знаете, алгебрата работи с променливи. В елементарната алгебра стойностите на променливите са числа; в булевата алгебра, стойностите на променливите са стойностите на истината: TRUE и FALSE. TRUE се обозначава с 1, а FALSE се означава с 0. В елементарната алгебра операциите, които извършваме са събиране, изваждане, умножение, деление и т.н. В булевата алгебра операциите са И, ИЛИ и НЕ.

В порта състоянието на две променливи, A и B, се сравнява в зависимост от булевия оператор.

Нека разгледаме първия булев оператор И. A И B се означава като AB. AB може да бъде TRUE само ако и A и B са верни. Не забравяйте, че TRUE се означава с 1. Вижте таблица 1. Само последният ред връща AB стойност TRUE или 1, защото само последният ред има TRUE (1) за A и TRUE (1) за B.

Таблица 1. Таблица на истинността за оператор И за две променливи
А Б А И Б (АВ) 0 0 0 0 1 0 1 0 0 1 1 1

Сега нека разгледаме втория булев оператор, ИЛИ. A OR B се означава като A+B. A+B може да бъде TRUE, ако A или B са верни. Не забравяйте, че TRUE се обозначава с 1 и вижте таблица 2. Последните три реда връщат стойност TRUE или 1, тъй като във всеки случай A или B имат стойност TRUE (1).

Таблица 2. Таблица на истинността за оператор ИЛИ за две променливи
А Б A ИЛИ B (A+B) 0 0 0 0 1 1 1 0 1 1 1 1

И накрая, нека разгледаме третия булев оператор, НЕ. Тук сме загрижени НЕ А. НЕ може да бъде вярно само ако А не да има стойност от TRUE или 1. Потърсете в Таблица 3. първия ред се връща на стойност TRUE или 1, защото сам по себе си е не да има стойност от ВЯРНО или 1.

Таблица 3. Допълнение или обратен оператор за една променлива
А НЕ А 0 1 1 0

Можем да приложим правилата на булевите оператори от таблици 1 до 3 към логически порти .

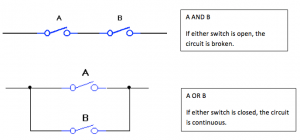
Фигура 2. Аналогията между булеви логически порти и електрически ключове

Погледнете горната верига на фигура 2. Ако някой от превключвателите е отворен, веригата е прекъсната. С други думи, веригата изисква както превключвателя A, така и превключвателя B да са затворени, което е същото като булевия оператор A И B или AB.

Сега погледнете долната верига на фигура 2, която е конфигурирана по различен начин. Тази схема изисква само превключвател A или ключ B да са затворени, което е същото като булевия оператор A OR B или A+B.

Полезността на тази концепция е показана в следния пример. Помислете за схема, която предупреждава шофьор, ако фаровете са включени и вратата на водача е отворена. Тази схема може да използва два входа към порта И:

Вход A – светлините са включени: Връща стойност от 0 (FALSE), ако светлините са изключени или стойност от 1 (TRUE), ако светлините са включени.

Вход B – Вратата на шофьора е отворена: Връща стойност от 0 (FALSE), ако вратата на шофьора е затворена, или стойност 1 (TRUE), ако вратата е отворена.

За да изведат 1 от порта И, и двете системи трябва да изведат 1. Нека визуализираме това в таблица на истинността:

Таблица 4. Таблица на истинността за пример превозно средство И порта
Вход A: светлините са включени Вход B: Шофьорската врата е отворена А И Б (АВ) 0 0 0 0 1 0 1 0 0 1 1 1

Ако някой от входовете е 0, ще се изведе 0. Изходът на порта И може да контролира състоянието на включване/изключване на транзистор със светлина или аларма на изходната страна на транзистора. По този начин, ако водачът излезе от превозното средство с включени светлини, той или тя ще бъде предупреден, че може да доведе до изтощен акумулатор, ако светлините не са изключени. Фигура 3 изобразява същия AND порт като логическа диаграма.

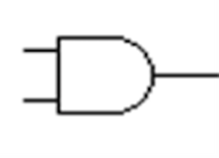
Фигура 3. И порта с два входа

Комбиниране на порти с повече от два входа

Лесно е да комбинирате порти с повече от два входа, като направите сравнение бит по бит. Във всеки от примерите по-долу, 0 означава FALSE или OFF, докато 1 означава TRUE или ON.

ПРИМЕР

Пример 1

010101010101 И

101010101010

равно на

000000000000

Защо? Защото нито едно от сравненията (на горните и долните числа) не съдържа 1 И 1. Следователно всяка стойност е 0.

ПРИМЕР

Пример 2

010101010101 ИЛИ

101010101010

равно на

111111111111

Защо? Защото всяко сравнение на горните и долните числа съдържа 0 ИЛИ 1. Следователно всяка стойност е 1.

ПРИМЕР

Пример 3

НЕ 000000000000

равно на

111111111111

Защо? Защото всяка стойност НЕ трябва да бъде 0. Следователно всяка стойност е 1.

Десетична, двоична и шестнадесетична бройна система

Хората използват основната 10 (десетична) бройна система, отдавна. Въпреки това, всяко число, по-голямо от 2, може ефективно да се използва като основа за число и система за броене. Всъщност електронните компютри използват основна 2 (двоична) бройна система на най-основното си ниво. Двоичната система естествено съответства на ON/OFF или TRUE/FALSE природата на техните електронни схеми и магнитни компоненти. В двоичната система числата се конструират с помощта на двете цифри, 0 и 1, и всяка от тези цифри представлява един бит данни. Други бройни системи са 8 (осмична) и 16 (шестнадесетична) бройна система. Ще обсъдим системите база 2 и база 16 и тяхното съответствие със системата база 10.

Нека започнем с основата 10 или десетичната система. За такава система са ни необходими десет уникални числа: 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9. Всички числа, по-високи от това и дроби по-малки от 1, могат да бъдат представени като степени на 10, както е показано в Таблица 5.

Таблица 5. Десетична бройна система
Мощност 10 3 10 2 10 1 10 0 . 10 -1 10 -2 10 -3 Стойност 1000 100 10 1 Десетична запетая 0.1 0,01 0,001

Двоичната система следва същото правило за местата, с изключение на това, че всяко място е с една степен на 2 по-голямо от мястото отдясно, както е показано в таблица 6.

Таблица 6. Двоична бройна система
Мощност 2 5 2 4 2 3 2 2 2 1 2 0 . 2 -1 2 -2 2 -3 Стойност 32 16 8 4 2 1 Двоична точка 1/2 = 0,5 1/4 = 0,25 1/8 = 0,125 Основа 2 100000 10000 1000 100 10 1 0.1 0,01 0,001

За шестнадесетичната система или системата с база 16 се нуждаем от символи за представяне на числата от 10 до 15. За тази система A се използва за 10, B за 11, C за 12, C за 13, D за 14 и E за 15 .

Таблица 7. Шестнадесетична бройна система
Мощност 16 3 16 2 16 1 16 0 . 16 -1 16 -2 Стойност 4096 256 16 1 Шестнадесетична точка 0,0625 0,00390625 База 16 1000 100 10 1 0.1 0,01

Таблица 8 показва сравнение на десетичните, двоични и шестнадесетични еквиваленти за първите 16 числа плюс 32 и 64. Използвайте правилата по-горе, за да разберете съответствията в таблицата.

Таблица 8. Съответствие между десетични, двоични и шестнадесетични числа
Десетична стойност Двоична стойност Шестнадесетична стойност 1 1 1 2 10 2 3 11 3 4 100 4 5 101 5 6 110 6 7 111 7 8 1000 8 9 1001 9 10 1010 г А 11 1011 Б 12 1100 ° С 13 1101 д 14 1110 г Е 15 1111 Ф 16 10000 10 32 100000 20 64 1000000 30

ПРИМЕР

10 в база 2 е 10102. Индексът указва база 2. Друг начин да се обозначи системата от числа на база 2 е да се постави малко b (за двоично) отдясно на число, т.е. 1010 _b .

За да докажете, че 1010 ₂ е равно на 10 в десетичната система, вижте таблица 6. Двоичното число 1010 ₂ съответства на едно 2 ³ , не 2 ² , едно 2 ¹ и не 2 ⁰ (единици). Това е 8 + 2 или 10, като по този начин се доказва, че 10 е еквивалентно на 1010 ₂ .

Допълнителни примери:

ПРИМЕР

10 в основа 16 е A _h . Индексът на A показва, че това е база 16 или шестнадесетично число.

ПРИМЕР

16 в база 16 е 10 _часа . Това е едно 16 и никакви.

ПРИМЕР

16 в база 2 е 10000 ₂ . Това е едно 2 ⁴ , няма 2 ³ , няма 2 ² , няма 2 ¹ и няма 2 ⁰ (единици).

ПРИМЕР

4096 в база 16 е 10000 _h . Това е едно 16 ³ , не 16 ² , не 16 ¹ и 16 ⁰ (единици).

Има правила за добавяне и изваждане на числа в основни системи, различни от десетични, но за нашите цели, стига да можете да преобразувате числа напред и назад между десетични, двоични и шестнадесетични, както и да можете да използвате по-познатата десетична система за всякакви изчисления.

 

Анализиране на данни от времеви серии за разстояние, скорост

Анализирайте променливите разстояние, скорост и ускорение като функция на мощност, енергия и време

Много системи за събиране на данни събират данни от времеви серии , които са данни, записани при промяна във времето. Времето е основна величина при регистрирането на данни. Графични мултиметри, цифрови осцилоскопи за съхранение, сензори и контролери, вградени в превозните средства, всички са примери за системи, които регистрират данни като функция на времето. Например скоростта на превозното средство зависи от времето: скоростта на превозното средство е промяната в разстоянието, разделена на промяната във времето. В този урок ще открием как да анализираме данни от времеви серии чрез начертаване на регистрираните променливи спрямо времето и изчисляване на статистически данни като средна, минимална стойност и максимална стойност за даден период от време.

Промяната в променливата в последователни подредени във времето наблюдения се използва за изчисляване на нови количества за по-задълбочено разбиране на системата.

Графиките на променливите спрямо времето дават бърз преглед на поведението на системата.

Разстояние, скорост и ускорение

В науката и инженерството, както и в ежедневието, трябва да използваме основните физични величини, свързани с движението: разстояние, скорост и ускорение. Например, за да изчислим времето, което ще отнеме за шофиране от дома до работа, се нуждаем от разстоянието за това пътуване и средната скорост по време на пътуването. Ако разстоянието е 10 мили и можем да шофираме със средна скорост от 40 мили в час, тогава пътуването ще отнеме 15 минути (10 мили X 1 час/40 мили = ¼ час или 15 минути).

Инженерите често събират данни за превозни средства като скорост на двигателя в обороти в минута (rpm), скорост на превозното средство и температура на двигателя като функция на времето. Тези данни в реално време се записват за даден цикъл на шофиране и се използват за анализи, за да се разбере работата на превозното средство. Такива данни могат да се използват за сравняване на работата на превозното средство със стандартите, както и за тестване на ефекта от промяната на определени параметри, свързани с работата на превозното средство, за подобряване на работата на превозното средство. Например, тестовите превозни средства се управляват по време на цикъл на шофиране във тестова процедура за измерване на емисиите на отработените газове, за да се провери дали превозното средство е в съответствие със стандартите. Цикълът на шофиране, използван за този тест, се нарича График за шофиране с градски динамометър (UDDS). За такъв тест, скоростта на превозното средство трябва да съответства на стандартна скорост по време на изпитването. Фигура 1 показва графика на скоростта спрямо времето за част от UDDS.

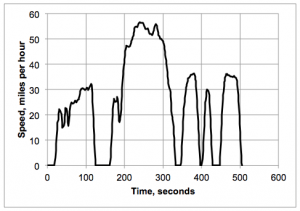
Фигура 1. Скорост в мили в час спрямо времето за първите 505 секунди от UDDS.

Цикълът на шофиране, показан на фигура 1, е проектиран да симулира типично пътуване от дома до работа. Тестът започва със студен старт, при който превозното средство се оставя през нощта, последвано от шофиране с ниска скорост в квартал, след това шофиране по магистрала и след това шофиране с по-ниска скорост близо до крайната дестинация. Има периоди, в които автомобилът работи на празен ход.

Нека анализираме данните, а именно данните за скоростта на времето за периода от 20 до 30 секунди, показани в таблица 1 по-долу. През този интервал има интересна промяна в скоростта. Забележете, че скоростта започва от 0 мили в час: превозното средство е спряно. След това превозното средство ускори от спирката до скорост от 21,7 мили в час в края на периода.

 

 

Таблица 1. Данни за скоростта за 10-секунден период на UDDS
Време, секунди Скорост, мили/час 20 0 21 3 22 5.9 23 8.6 24 11.5 25 14.3 26 16.9 27 17.3 28 18.1 29 20.7 30 21.7

Таблица 2 по-долу показва същите данни, но с някои допълнителни колони и някои изчисления въз основа на тези добавени колони. Първо, данните за времето в секунди бяха копирани до оригиналните данни за времето, но с премахнато първо наблюдение на времето. По този начин времето във втората колона е изоставане от първоначалните времеви данни, които ще наречем лаг (време). За UDDS данните, които са посочени с интервал от една секунда между последователни наблюдения, изоставането (времето) винаги е една секунда. Такава систематична времева разлика не е необходима при анализа; последователните наблюдения могат да се различават за произволно време и анализът ще остане същият. Третата колона в таблица 2 показва разликата между втората и първата колона. Това се нарича Δ време, съкратено Δt,

Δt = лаг (време) – време

Петата колона показва данните за скоростта със закъснение от едно наблюдение. Разликата в скоростта и закъснението в скоростта, Δ скорост, е показана в шестата колона.

Δ скорост = изоставане (скорост) – скорост

Последната колона от дясната страна на таблица 2 показва Δскорост/Δt. Промяната в скоростта, разделена на промяната във времето, е ускорението на превозното средство. Ускорението е много важна променлива във физиката и се използва при изчисляване на силата, необходима за ускоряване на масата на превозното средство. Разходът на гориво на автомобила и емисиите от ауспуха на автомобила зависят силно от ускорението.

Таблица 2. Данни за скоростта на времето от Таблица 1, подредени за анализиране на разликата в последователните наблюдения
Време Време за закъснение Δ време Скорост Скорост на забавяне Δ скорост Δ скорост/Δt секунди секунди секунди мили/час мили/час мили/час мили/час/секунда 20 21 1 0 3 3 3 21 22 1 3 5.9 2.9 2.9 22 23 1 5.9 8.6 2.7 2.7 23 24 1 8.6 11.5 2.9 2.9 24 25 1 11.5 14.3 2.8 2.8 25 26 1 14.3 16.9 2.6 2.6 26 27 1 16.9 17.3 0.4 0.4 27 28 1 17.3 18.1 0.8 0.8 28 29 1 18.1 20.7 2.6 2.6 29 30 1 20.7 21.7 1 1 30 21.7

Таблица 3 по-долу показва друг анализ на данните в Таблица 1. В Таблица 3 времето и скоростта се използват за изчисляване на разстоянието, което превозното средство е изминало през всяка секунда от 10-секундния интервал от време, както и общият пробег през интервала . Данните в третата колона се изчисляват чрез промяна на мерните единици от мили/час на футове/секунда. Това е проста математика, използваща броя на футовете в една миля и броя на секундите в един час:

1 миля/час x 5280 фута/миля x 3600 секунди/час = 1,467 фута/секунда

Така колона 3 е колона 2 по 1,467.

Определението за скорост е

Скорост = промяната в разстоянието ÷ промяната във времето = Δd ÷Δt

Така че чрез пренареждане:

Δd = скорост X Δt

Промяната във времето между последователни наблюдения в Таблица 3 е една секунда, така че разстоянието е равно на скоростта във футове/секунда по 1 секунда. Тази скорост е показана в четвъртата колона на Таблица 3. И накрая, общото разстояние през интервала е сумата от разстоянията за всеки интервал от една секунда. Общото разстояние до всяка времева точка е показано в колона 5 на Таблица 3.

При математическия анализ на тези данни от времеви ред, ние изчислихме разликите в променливите във времето, за да извлечем основните физически променливи: разстояние, скорост и ускорение. За да завърши анализа, инженерът може да начертае всяка от тези променливи спрямо времето, както и да изчисли други променливи като сила (сила = маса X ускорение) или енергия (енергия = сила X преместено разстояние). И накрая, средните стойности на променливите за целия тест, показан на фигура 1, могат да бъдат изчислени, както и минималните и максималните стойности. Например, средната скорост за данните от фигура 1 е сумата от отделните скорости, разделена на броя на наблюденията. Тази стойност е 25,5 мили в час. Максималната скорост по време на теста е 56,7 мили в час,

Таблица 3. Данни за скоростта на времето от таблица 1, подредени за анализ на изминатото разстояние във всеки интервал от време
Време Скорост Скорост Разстояние Общо разстояние секунди мили/час фута/секунда крака крака 20 0 0,00 0,00 0,00 21 3 4.40 4.40 4.40 22 5.9 8,65 8,65 13.05 23 8.6 12.61 12.61 25.67 24 11.5 16.87 16.87 42,53 25 14.3 20,97 20,97 63,51 26 16.9 24,79 24,79 88,29 27 17.3 25.37 25.37 113,67 28 18.1 26.55 26.55 140,21 29 20.7 30.36 30.36 170,57 30 21.7 31,83 31,83 202,40

Друг пример за променливи, които са свързани във времето, включва връзката между мощност, енергия и време. Количеството енергия, използвано в даден интервал от време, е мощността. Мощността често се измерва в киловати (kW), времето в часове (h) и енергията в киловатчасове (kWh). Ако една крушка консумира постоянна мощност от 100 W за 10 часа, тя използва 1000 вата часа или 1 kWh електрическа енергия. По този начин, ако измерваме време, напрежение и ток, можем да изчислим мощност (напрежение X ток). Ако имаме такива данни като функция на времето, същият анализ, описан по-горе, може да се използва за изчисляване на използваната енергия за всеки интервал от време (мощност X Δt) и общата консумирана енергия от началото на периода до края.